Electricity and Magnetism Exam
Help Questions
AP Physics C: Electricity and Magnetism › Electricity and Magnetism Exam
A proton moves in a straight line for a distance of 

The charge of a proton is 
Explanation
Potential difference is given by the change in voltage
Work done by an electric field is equal to the product of the electric force and the distance travelled. Electric force is equal to the product of the charge and the electric field strength.
The charges cancel, and we are able to solve for the potential difference.
If two identical parallel plate capacitors of capacitance 

Explanation
Relevant equations:
Use the series equation, replacing C1 and C2 with the given constant C:
This agrees with the general rule that the equivalent capacitance in series is less than the capacitance of any of the individual capacitors.
A proton moves in a straight line for a distance of 

The charge of a proton is 
Explanation
Potential difference is given by the change in voltage
Work done by an electric field is equal to the product of the electric force and the distance travelled. Electric force is equal to the product of the charge and the electric field strength.
The charges cancel, and we are able to solve for the potential difference.
If two identical parallel plate capacitors of capacitance 

Explanation
Relevant equations:
Use the series equation, replacing C1 and C2 with the given constant C:
This agrees with the general rule that the equivalent capacitance in series is less than the capacitance of any of the individual capacitors.
If two identical parallel plate capacitors of capacitance 

Explanation
Relevant equations:
Use the series equation, replacing C1 and C2 with the given constant C:
This agrees with the general rule that the equivalent capacitance in series is less than the capacitance of any of the individual capacitors.
If two identical parallel plate capacitors of capacitance 

Explanation
Relevant equations:
Use the series equation, replacing C1 and C2 with the given constant C:
This agrees with the general rule that the equivalent capacitance in series is less than the capacitance of any of the individual capacitors.
A proton moves in a straight line for a distance of 

The charge of a proton is 
Explanation
Potential difference is given by the change in voltage
Work done by an electric field is equal to the product of the electric force and the distance travelled. Electric force is equal to the product of the charge and the electric field strength.
The charges cancel, and we are able to solve for the potential difference.
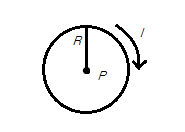
Consider a current-carrying loop with current 


What would happen to the magnetic field at point 
The new magnetic field would be eight times as strong as the original
The new magnetic field would reverse direction
The new magnetic field would be four times as strong as the original
The new magnetic field would be eight times weaker than the original
The new magnetic field would be four times weaker than the original
Explanation
The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:
Using out altered values, we can derive a ratio to determine the change in magnetic field.
The resulting field will be eight times stronger than the original.

Consider a current-carrying loop with current 


What would happen to the magnetic field at point 
The new magnetic field would be eight times as strong as the original
The new magnetic field would reverse direction
The new magnetic field would be four times as strong as the original
The new magnetic field would be eight times weaker than the original
The new magnetic field would be four times weaker than the original
Explanation
The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:
Using out altered values, we can derive a ratio to determine the change in magnetic field.
The resulting field will be eight times stronger than the original.

Consider a current-carrying loop with current 


What would happen to the magnetic field at point 
The new magnetic field would be eight times as strong as the original
The new magnetic field would reverse direction
The new magnetic field would be four times as strong as the original
The new magnetic field would be eight times weaker than the original
The new magnetic field would be four times weaker than the original
Explanation
The current flowing clockwise through the wire will induce a magentic field directed into the screen. The magnitude of such a magnetic field is given by the equation:
Using out altered values, we can derive a ratio to determine the change in magnetic field.
The resulting field will be eight times stronger than the original.

















