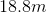Pressure
Help Questions
AP Physics 2 › Pressure
Suppose that a barometer is filled with water, as shown in the diagram below. If this barometer's column has a height of 
Note: Mercury has a specific gravity of 

Explanation
For this question, we're asked to see how the height of a barometer's column will change once the liquid changes from water to mercury.
Barometers are a measure of atmospheric pressure. As the ambient pressure pushes down on the surface of the liquid, this pressure is transmitted throughout the liquid, such that it causes the liquid level in the water to rise. As the ambient pressure increases, the column in the barometer climbs.
We'll need to use the equation for pressure as it relates to density and height.
Since the ambient pressure is the same in both instances, we can set these terms equal to each other. That is to say, it doesn't matter which liquid is being used in the column, because both of them will feel the same pressure from the atmosphere.
Next, we can rearrange the above expression to isolate the term for the height in the mercury column.
Finally, we can plug in the terms given to us in the question stem to arrive at our answer.
Suppose that you accidentally let go of a helium balloon, and it begins to rise higher and higher into the sky. The balloon will continue to rise until which of the following takes place?
The density of the air inside the balloon is equal to the density of the surrounding air.
The temperature of the air inside the balloon is equal to the temperature of the surrounding air.
The mass of the air inside the balloon is equal to the mass of the surrounding air.
The weight of the air inside the balloon is equal to the weight of the surrounding air.
The balloon will continue to rise indefinitely.
Explanation
To answer this question, it's useful to think of this conceptually as the balloon being "submerged" in the atmosphere. Remember, buoyant forces refer to the force caused by the displacement of a fluid, and both liquids and gasses count as fluids. Thus, in this case, the balloon can be thought of as submerged in a fluid in the same way that any object can be submerged in a liquid such as water.
We're trying to look for the point at which the balloon stops rising. This is analogous to a situation in which the balloon is "floating" in the fluid. In such a case, the upward and downward forces are equal and balance each other out.
So now, we need to identify the upward and downward forces acting on the balloon and set them equal to each other. The upward force will be the buoyant force due to the displacement of air from the atmosphere. The downward force will be the weight of the balloon.
We can further rewrite the mass of the balloon in terms of its weight and density.
Canceling out the gravity term, we obtain:
Next, it's important to realize that the volume of atmosphere being displaced is exactly the same as the volume of the balloon, since it is the balloon that is causing the displacement of air in the atmosphere. Thus:
Furthermore, because these two values are equal, we can cancel them out in the above expression to obtain the following.
Here, we have shown that once the density of the balloon becomes equal to that of the surrounding atmosphere, it will cease rising.
A U-shaped tube is filled with water, however the openings on either ends have different cross-sectional areas of 



Explanation
The following formula on pressure and area is used:
We substitute our known values and solve for F2 to obtain the output force:
Therefore the correct answer is 
Paul weighs 

Explanation
Pressure is force divided by area. The force Paul applies is 
Suppose that a force of 

Explanation
This is a fairly straight-forward question, providing us with a force vector that is acting upon a surface and asking us for the pressure.
First and foremost, we can examine the equation for pressure:
Next, we'll need to figure out the sign convention for pressure. Based on the above equation, it may seem like if we plug in a negative value for pressure and a positive value for area, we'll get a negative value for pressure. However, this is not the case.
As it turns out, pressure is a scalar quantity. The reason for this is that when any force acts on a surface, it is acting perpendicularly to that surface. Therefore, the direction in which the force is acting is dependent on how the surface is oriented. No matter which way you orient the surface, the force that is acting on that surface will always be perpendicular. Consequently, pressure is essentially just a proportionality between force and area that has no bearing on direction.
At what depth within a salt water solution will the gauge pressure be equal to three times the atmospheric pressure?
Explanation
We can begin this problem by writing the equation for pressure.
We have to remember that the value of atmospheric pressure is equal to 1atm, which is also equal to 101325Pa.
Now, if we set the gauge pressure equal to three times the atmospheric pressure, we can solve for the depth.
Suppose that a person is swimming in the ocean, which has saltwater with a density of 
Explanation
This question is presenting us with a situation in which an object (a person) submerged in a liquid is experiencing pressure. To solve for the correct pressure, we'll need to take a few things into account.
First, we'll need to consider the density of the liquid. In this case, we're told that the liquid is saltwater, and we're given the density in the question stem. Second, we'll need to consider how far below the surface of the liquid our object is. Again, this value is given to us in the question stem. And third, we also need to remember that there is a pressure above the liquid, which is the pressure coming from the atmosphere. This value (which should be committed to memory) is 

Putting all these considerations together, we have an equation that we can use to calculate the pressure.
Plug in the values that we know and solve for total pressure.
Calculate the difference in pressure, 

Explanation
The pressure at the lake's surface is just the atmospheric pressure, 



We can then substitute the values in to arrive at the answer in 
Recall that this pressure is known as gauge pressure, and that the total pressure at the point underwater in the lake includes gauge pressure and atmospheric pressure.
A cube with a mass of 

Explanation
The formula for pressure is given as:
Where 


Therefore the correct answer is
Someone who is down on their luck throws a dime down a deep well. At time 



Explanation
Given the hydrostatic pressure, we can calculate the depth that this occurs at:
Rearranging for height:
Plugging in our values, we get:
We can then use the following kinematics equation to determine how much time has passed:
If we designate the downward direction as positive and plugging in values to the kinematics equation, we get:
Rearranging, we get:
Since we can't have a negative time, the first one is the answer.