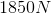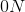Fluid Statics
Help Questions
AP Physics 2 › Fluid Statics
Seawater density:
A baseball has a mass of 

None of these
Explanation
Solving for
Plugging in values
If the circumference is 
Seawater density:
A baseball has a mass of 

None of these
Explanation
Solving for
Plugging in values
If the circumference is 
What is the net force on a ball of mass 

Explanation
The buoyant force on the ball is simply the weight of water displaced by the ball:
The force of gravity on the ball is:
These forces oppose each other, so we can say:
What is the net force on a ball of mass 

Explanation
The buoyant force on the ball is simply the weight of water displaced by the ball:
The force of gravity on the ball is:
These forces oppose each other, so we can say:
Suppose that a barometer is filled with water, as shown in the diagram below. If this barometer's column has a height of 
Note: Mercury has a specific gravity of 

Explanation
For this question, we're asked to see how the height of a barometer's column will change once the liquid changes from water to mercury.
Barometers are a measure of atmospheric pressure. As the ambient pressure pushes down on the surface of the liquid, this pressure is transmitted throughout the liquid, such that it causes the liquid level in the water to rise. As the ambient pressure increases, the column in the barometer climbs.
We'll need to use the equation for pressure as it relates to density and height.
Since the ambient pressure is the same in both instances, we can set these terms equal to each other. That is to say, it doesn't matter which liquid is being used in the column, because both of them will feel the same pressure from the atmosphere.
Next, we can rearrange the above expression to isolate the term for the height in the mercury column.
Finally, we can plug in the terms given to us in the question stem to arrive at our answer.
Suppose that a barometer is filled with water, as shown in the diagram below. If this barometer's column has a height of 
Note: Mercury has a specific gravity of 

Explanation
For this question, we're asked to see how the height of a barometer's column will change once the liquid changes from water to mercury.
Barometers are a measure of atmospheric pressure. As the ambient pressure pushes down on the surface of the liquid, this pressure is transmitted throughout the liquid, such that it causes the liquid level in the water to rise. As the ambient pressure increases, the column in the barometer climbs.
We'll need to use the equation for pressure as it relates to density and height.
Since the ambient pressure is the same in both instances, we can set these terms equal to each other. That is to say, it doesn't matter which liquid is being used in the column, because both of them will feel the same pressure from the atmosphere.
Next, we can rearrange the above expression to isolate the term for the height in the mercury column.
Finally, we can plug in the terms given to us in the question stem to arrive at our answer.
A spherical ball of density 

Explanation
We can use Archimedes's Principle to solve this problem which states that the upward buoyant force on an object is equal to the weight of the fluid that the object displaces. Therefore, if an object is floating, the upward buoyant force is equal to the weight of the object. So, let's begin by calculating that. We are given the radius of the object and told that it is a sphere. Therefore, we can use the expression for the volume of a sphere:
Now multiplying this by the density, we get:
This is also going to be the mass of the water displaced. We can therefore calculate the volume of water displaced:
A ball of mass 


None of these
Explanation
The volume displaced will equal the volume of the ball.
A spherical ball of density 

Explanation
We can use Archimedes's Principle to solve this problem which states that the upward buoyant force on an object is equal to the weight of the fluid that the object displaces. Therefore, if an object is floating, the upward buoyant force is equal to the weight of the object. So, let's begin by calculating that. We are given the radius of the object and told that it is a sphere. Therefore, we can use the expression for the volume of a sphere:
Now multiplying this by the density, we get:
This is also going to be the mass of the water displaced. We can therefore calculate the volume of water displaced:
A ball of mass 


None of these
Explanation
The volume displaced will equal the volume of the ball.