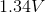Electric Potential Energy
Help Questions
AP Physics 2 › Electric Potential Energy
Suppose that a point charge of 1 Coulomb undergoes a change in which it is moved from point A to point B while in the presence of an external electric field. During this transposition, it undergoes a voltage change of 
Explanation
In order to solve for electrical potential energy, we'll need to remember the equation for it.
In the above expression, 



Furthermore, we can remember the equation for voltage:
With both these equations in mind, we can combine the two:
This above expression tells us that the electrical potential energy of a system is directly proportional to the voltage change and to the charge of the test charge that is undergoing the voltage change.
Plug in the values and solve for electrical potential energy:
What is the electric potential between two terminals of a cell if it requires 

Explanation
Write the formula for the potential difference.
Substitute the work and charge. The unit is in volts.


Explanation
We need to find the voltage, and we have the resistance, so if we can find the current, then we can use Ohm's Law to find the voltage.
The definition of current is amount of charge that flows through a point in 
We're told how many electrons have passed through a resistor, and we know how much charge a single electron has. If we convert the number of electrons into total amount of charge, we can divide that number by the amount of time in seconds to find the current.
Now we have the amount of charge in 
Now that we have the current, we can use Ohm's Law to find the voltage.
Therefore, the potential difference is 2.96V.
In a region of space, there is an electric field whose magnitude is 

Cannot be determined
Explanation
This problem is solved using the work-kinetic energy theory: 
Since an electron has a negative charge, decreasing potential increases its kinetic energy, the opposite of what would happen to a proton with its positive charge. Combine these equations:
Plug in known values and solve
There is an electric field of between two parallel plates of 

Find the electric potential energy of a particle of charge 
None of these
Explanation
Use the equations for potential electric energy and electric potential:
Substitute.
Plug in known values and solve.
A proton is placed into an electric potential of 
None of these
Explanation
Conservation of energy:
Assuming no external work done
Electric potential energy:
Solving for velocity:
Plugging in values:
Determine the electric potential energy of a 

None of these
Explanation
Converting units:
Use the equation for electric potential energy:
A 



None of these
Explanation
Force in an electric field:
Using conservation of energy, assuming no external work on system:
Definition of electric potential energy:
Definition of electric potential:
Combining equations:
Assuming final velocity is zero:

Converting 
Plugging in values:
Solving for
A ball of mass 


None of these
Explanation
Force in an electric field:
Using conservation of energy, assuming no external work on system:
Definition of electric potential energy:
Combining equations:
Assuming initial velocity and final electric potential is zero:
The charge, 
Converting 

A student is working on a laboratory exercise in which she measures the electric potential (voltage) at several points in an electric field. Before graphing the potential isolines, she measures the electric potential to be 3V at one point in the field and 7V at a point 3cm from the first point. What is the average electric field strength between the two points the student measured?
Explanation
Electric field strength is the slope of the electric potential:
Remember to convert into SI units (meters):