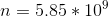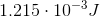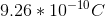Circuit Components
Help Questions
AP Physics 2 › Circuit Components
Consider the given diagram. If 

None of these
Explanation
The voltage rise through the source must be the same as the drop through the capacitor.
The voltage drop across the capacitor is the equal to the electric field multiplied by the distance.
Combine equations and find the electric field:
Convert mm to m and plugg in values:
Use the electric field in a capacitor equation:
Convert 

The magnitude of total charge on the positive plate is equal to the total charge on the negative plate, so to find the number of excess elections:
A 

None of the other answers is correct
Explanation
To find the amount of energy stored in a capactior, we use the equation

We're given the capacitance (

You have 3 resistors in parallel with each other. What can you say for certain about the total resistance of the circuit?
The total resistance is less than any individual resistor.
The total resistance is higher than any individual resistor.
The total resistance is somwhere between the highest resistor and the lowest resistor.
Nothing can be said for certain about the total resistance.
The total resistance is equal to the arithmetic mean of the resistors.
Explanation
Because the resistors are in parallel, we can use the equation for finding the total resistance.
Using this equation, any positive numbers we plug into the equation for the resistances will yield a number that is less than any of the resistors individually. Using this property allows for many more resistances to be achieved besides the individual resistors one may have.
Two parallel conducting plates separated by a distance 

The electric charge on the plates is halved
The potential difference between the plates is doubled
The capacitance is unchanged
The potential difference between the plates is halved
The electric charge on the plates is doubled
Explanation
The equation for capacitance of parallel conducting plates is:
When the distance is doubled, the capacitance changes to:
The battery is still connected to the plates, the potential difference is unchanged. Because 

You have 3 resistors in parallel with each other. What can you say for certain about the total resistance of the circuit?
The total resistance is less than any individual resistor.
The total resistance is higher than any individual resistor.
The total resistance is somwhere between the highest resistor and the lowest resistor.
Nothing can be said for certain about the total resistance.
The total resistance is equal to the arithmetic mean of the resistors.
Explanation
Because the resistors are in parallel, we can use the equation for finding the total resistance.
Using this equation, any positive numbers we plug into the equation for the resistances will yield a number that is less than any of the resistors individually. Using this property allows for many more resistances to be achieved besides the individual resistors one may have.
Two parallel conducting plates separated by a distance 

The electric charge on the plates is halved
The potential difference between the plates is doubled
The capacitance is unchanged
The potential difference between the plates is halved
The electric charge on the plates is doubled
Explanation
The equation for capacitance of parallel conducting plates is:
When the distance is doubled, the capacitance changes to:
The battery is still connected to the plates, the potential difference is unchanged. Because 

You have 3 capacitors in series. Their capcitance's are 


None of the other answers is correct
Explanation
To find the total capacitance of capacitors in series, you use the following equation:

Our values for 


The answer we have is the inverse of this. Therefore, the total capacitance is 
Consider the given diagram. If 


Explanation
The voltage rise through the source must be the same as the drop through the capacitor.
The voltage drop across the capacitor is the equal to the electric field multiplied by the distance.
Combine equations and solve for the electric field:
Convert mm to m and plug in values:
Using the electric field in a capacitor equation:
Rearrange to solve for the charge:
Convert 

Consider the given diagram. If 

None of these
Explanation
The voltage rise through the source must be the same as the drop through the capacitor.
The voltage drop across the capacitor is the equal to the electric field multiplied by the distance.
Combine equations and find the electric field:
Convert mm to m and plugg in values:
Use the electric field in a capacitor equation:
Convert 

The magnitude of total charge on the positive plate is equal to the total charge on the negative plate, so to find the number of excess elections:
A 

None of the other answers is correct
Explanation
To find the amount of energy stored in a capactior, we use the equation

We're given the capacitance (