Electrostatics
Help Questions
AP Physics 1 › Electrostatics
An excess charge of 



Explanation
Two principal realizations help with solving this problem, both derived from Gauss’ law for electricity:
-
The excess charge on an ideal conducting sphere is uniformly distributed over its surface
-
A uniform shell of charge acts, in terms of electric force, as if all the charge were contained in a point charge at the sphere’s center
With these realizations, an application of Coulomb’s law answers the question. If 

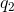
In this equation, 



Using the given values in this equation, we can calculate the generated force:
An excess charge of 



Explanation
Two principal realizations help with solving this problem, both derived from Gauss’ law for electricity:
-
The excess charge on an ideal conducting sphere is uniformly distributed over its surface
-
A uniform shell of charge acts, in terms of electric force, as if all the charge were contained in a point charge at the sphere’s center
With these realizations, an application of Coulomb’s law answers the question. If 

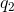
In this equation, 



Using the given values in this equation, we can calculate the generated force:
What is the magnitude of the electric force between two charged metals that are 3m apart, that have absolute value of the charges being 1C and 3C?
Explanation
We are given all the necessary information to find the magnitude of the electric force by using Coulomb's law:
Where 




What is the magnitude of the electric force between two charged metals that are 3m apart, that have absolute value of the charges being 1C and 3C?
Explanation
We are given all the necessary information to find the magnitude of the electric force by using Coulomb's law:
Where 




Determine the strength of a force of proton on another proton in the nucleus if they are 
Explanation
Use Coulomb's law:




Determine the strength of a force of proton on another proton in the nucleus if they are 
Explanation
Use Coulomb's law:




An electric field line is point from the left towards the right. Where will an electron move when placed in the field?
Towards the left
Towards the right
Upward
Downward
It will not move
Explanation
The electron will move towards the left because electric field lines always point towards the negative charge. The electron is negatively charged and will oppose the negative electric field on the right and move towards the positive end on the left.
Therefore the correct answer is that the electron will move to the left.
An electric field line is point from the left towards the right. Where will an electron move when placed in the field?
Towards the left
Towards the right
Upward
Downward
It will not move
Explanation
The electron will move towards the left because electric field lines always point towards the negative charge. The electron is negatively charged and will oppose the negative electric field on the right and move towards the positive end on the left.
Therefore the correct answer is that the electron will move to the left.
Two protons are at a distance 



Explanation
Coulomb's law shows that the force between two charged particles is inversely proportional to the square of the distance between the particles.
If the distance between the charges is reduced by 



If we have 2 charges, 








Explanation
Use Coulomb's law.
Plug in known values and solve.
Note that this force is positive, which means it's repulsive.







































