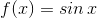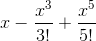Maclaurin Series
Help Questions
AP Calculus BC › Maclaurin Series
For which of the following functions can the Maclaurin series representation be expressed in four or fewer non-zero terms?
Explanation
Recall the Maclaurin series formula:
Despite being a 5th degree polynomial recall that the Maclaurin series for any polynomial is just the polynomial itself, so this function's Taylor series is identical to itself with two non-zero terms.
The only function that has four or fewer terms is 

Find the value of the infinite series.
Infinite series does not converge.
Explanation
The series


but the series we want to simplify starts at 



So now we have 


So then we have:
Explanation
Find the Maclaurin Series of the function
up to the fifth degree.
Explanation
The formula for an i-th degree Maclaurin Polynomial is
For the fifth degree polynomial, we must evaluate the function up to its fifth derivative.
The summation becomes
And substituting for the values of the function and the first five derivative values, we get the Maclaurin Polynomial
Write the first two terms of the Maclaurin series for the following function:
Explanation
The Maclaurin series for any function is simply the Taylor series for the function about a=0:
For the first two terms (n=0, 1) we must find the zeroth and first derivative of the function. The zeroth derivative is just the function itself.
Now, using the above formula, write out the first two terms:
Explanation
Explanation
Explanation
What is the value of the following infinite series?
Explanation
We can recognize this series as 
with the value 


So then we have

Write out the first three terms for the Maclaurin series of the following function:
Explanation
The Maclaurin series for any function is simply the Taylor series of the function about a=0:
We first must find the zeroth, first, and second derivative of the function (for n=0, 1, and 2). The zeroth derivative is the function itself:
The derivatives were found using the following rules:

Now, we just use the formula, with