Fundamental Theorem of Calculus and Techniques of Antidifferentiation
Help Questions
AP Calculus BC › Fundamental Theorem of Calculus and Techniques of Antidifferentiation
Evaluate 
Explanation
By the Formula Rule, we know that 

Continuing the calculation:
By the Power Rule for Integrals, 



So,
As 
Evaluate the following integral:
Explanation
This integral is improper because the lower bound creates a zero in the denominator. To integrate, we must use a limit:
The following rule was used:
Now, the definite part of the integral:
The natural logarithm of 1 equals zero, and as the natural logarithm approaches zero, the function goes to negative infinity. The negative sign in front of the function makes it go to infinity.
Evaluate the following integral:
Explanation
The integral is improper because of the upper limit of integration (creates zero in the denominator of the function being integrated). So, we have to do the following:
We evaluate the limit from the left side because the upper limit of integration was the one that caused problems.
Now, to integrate we must do a substitution, but this also means changing the limit:
The derivative was perfomed using the following rule:
Now, rearrange, and rewrite the limit in terms of our new t value, which originally was 
Next, perform the definite integration, keeping the limit:
The integration was performed using the following rule:
Now, when we evaluate the limit, we notice that the natural log function, as it approaches zero, approaches negative infinity. The fact that there is a coefficient on the limit or the additional term being subtracted are insignificant compared to the negative infinity term. So, our final answer is 
he Laplace Transform is an integral transform that converts functions from the time domain 



Where 



Give the Laplace Transform of ![\frac{\mathrm{d} }{\mathrm{d} t}[f(t)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/834351/gif.latex)
Explanation
The Laplace Transform of the derivative is given by:
Using integration by parts,
Let 
The first term becomes
and the second term becomes
The Laplace Transform therefore becomes:
Explanation
In order to evaluate this integral, we will need to use partial fraction decomposition.
Multiply both sides of the equation by the common denominator, which is
This means that 
The answer is 
Evaluate
Explanation
Use the fundamental theorem of calculus to evaluate:
Explanation
In order to evaluate this integral, we will need to use partial fraction decomposition.
Multiply both sides of the equation by the common denominator, which is
This means that 
The answer is 
Evaluate the improper integral:
The integral does not converge.
Explanation
First, we will perform an integration by parts on the indefinite integral

Let 

Then,


Also,

Therefore,
The antiderivative of 
and


Evaluate
Explanation
Use the fundamental theorem of calculus to evaluate:
Evaluate:
The integral does not converge
Explanation
First, we will find the indefinite integral, 
We will let 

Then,


and
Now, this expression evaluated at 

At 

We can use L'Hospital's rule to find its limit as 


Therefore,











![\lim_{b\rightarrow \infty }3[-{\frac{1}{x}}]_{1}^b](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/382325/gif.latex)
![=\lim_{b\rightarrow \infty }3[-{\frac{1}{b}-(-\frac{1}{1}})]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/382326/gif.latex)
![=\lim_{b\rightarrow \infty }3[-{\frac{1}{b}+1]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/382327/gif.latex)
![\lim_{b\rightarrow \infty }3[-{\frac{1}{b}+1]=3(0+1)=3](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/382329/gif.latex)

















![\frac{1}{2}\lim_{t\rightarrow 4^{-}}[\ln\left |(t-4) \right |-\ln\left |4 \right |]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/409030/gif.latex)







![\int_{0}^{\infty} UdV= [UV]_{0}^{\infty}-\int_{0}^{\infty} VdU](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/834362/gif.latex)

![[e^{-st}*f(t) ]_{0}^{\infty}-\int_{0}^{\infty}(-s)e^{-st}*f(t) dt](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/834365/gif.latex)




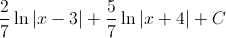

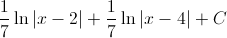



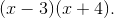






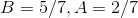
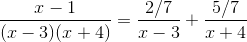
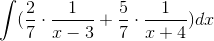









![\frac{1}{3} (6-3)^3 - [ \frac{1}{3}(0-3)^3] = \frac{1}{3} (3)^3 - \frac{1}{3} (-3)^3](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/854677/gif.latex)




































![=\lim _{b\rightarrow 0}\left [ \left.\begin{matrix} \frac{ x ^{2}\ln{x}}{2} - \frac{x^{2}}{4} \ \ \end{matrix}\right| \begin{matrix} 1\ \ b \end{matrix} \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/180705/gif.latex)

