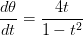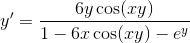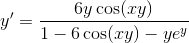Applications of Derivatives
Help Questions
AP Calculus AB › Applications of Derivatives
Given that 
Explanation
To find the derivative with respect to y, we use implicit differentiation, which is an application of the chain rule.
Concrete at a factory flows according to the following theoretical model:
What is the rate of change of the concrete flow?
Explanation
The rate of change of the concrete flow is given by the first derivative of the concrete flow function:
and was found using the following rules:


A body's position "s" is given by the equation:

a) Find the body's speed at the endpoints of the given interval
b) Find the body's acceleration at the endpoints of the given interval
Explanation
We are given the function describing the position of the body given a time "t":
We are also given the interval that the function can be applied over:
First, we are tasked to find the speed of the body at each of the endpoints (0 and 2 seconds, respectively).
To figure this, we must understand that speed is the absolute value of velocity.
To find the velocity function, we must take the derivative of the position function with respect to time:
Now that we have the function of velocity given a time "t", we can find the speed of the body given a time "t" by simply taking the absolute value of the velocity function.
Now, to find the speed of the endpoints:
We can repeat the same process to find the speed at 2 seconds.
For part a, the speeds at 0 and 2 seconds are 3 and 1 \[m/s\], respectively.
Part b asks us to find the acceleration at the endpoint times (0 and 2 seconds). To do this, we must first understand that to find acceleration at a time "t", we must take the derivative, with respect to time, of the velocity function.
From part a, we found the velocity function:
Thus, to find acceleration, we derive this function with respect to time.
The result of our derivation tells us that no matter what time is plugged into the function, the acceleration shall always return 2\[m/s^2\].
So, for part b, the acceleration at 0 and 2 seconds are 2 and 2 \[m/s^2\], respectively.
If p(t) gives the position of an asteroid as a function of time, find the function which models the velocity of the asteroid as a function of time.
Explanation
If p(t) gives the position of an asteroid as a function of time, find the function which models the velocity of the asteroid as a function of time.
Begin by recalling that velocity is the first derivative of position. So all we need to do is find the first derivative of our position function.
Recall that the derivative of sine is cosine, and that the derivative of polynomials can be found by multiplying each term by its exponent, and decreasing the exponent by 1.
Starting with:
We get:
Find the intervals on which 
Explanation
To find the intervals where the function is increasing, we need to find the points at which its slope changes from positive to negative and vice versa. The first derivative, which is the slope at any point, will help us.
First, we find the derivative of 
Also, the constant multiple rule will apply to the coefficients of each term. The constant multiple rule simply says that any constant factor of a term will "carry" to the derivative of that term. For example:
Lastly, the derivative of a constant is zero. This will result in the last term, 
Applying these rules, we find the derivative
Where the derivative is positive (blue line in graph), the tangent line to the original function is angled up. Where the derivative is negative (red line in graph), the slope of the tangent line is angled down.

The points where the tangent line's slope transitions from negative to positive or vice versa, are called the critical points. At these points, the tangent line becomes a horizontal line with a slope of zero (green line in graph). In other words, the "critical points" occur when the derivative is zero. These points will be the endpoints of our intervals of increasing and decreasing. To find the critical points, we will set the derivative equal to zero and solve for x. In this problem factoring is the best method:



Now that we have found the critical points, we need to know whether the original function is increasing or decreasing in the intervals between them. We will do so by testing a point in each interval and determining whether the derivative is positive or negative at that point. This is called the first derivative line test.
For the interval 

(Note: I will use the factored form of the derivative, but we could also use the polynomial version. Both will give the same result)
Since the derivative is negative at this point, we can conclude that the derivative is negative for the whole interval. Thus, the original function is decreasing on 
For the interval 

Since the derivative is positive at this point, we can again conclude that the derivative is positive for the whole interval. Thus, the original function is increasing on 
For the interval 

Since the derivative is negative at this point, we can again conclude that the derivative is negative for the whole interval. Thus, the original function is decreasing on 
Lastly, for the interval 

Since the derivative is positive at this point, we know that the derivative is positive for the whole interval. Thus the original function is increasing on 
From these 4 results, we now know the answer. The function is increasing on the intervals 
Find the intervals on which 
Explanation
To find the intervals where the function is increasing, we need to find the points at which its slope changes from positive to negative and vice versa. The first derivative, which is the slope at any point, will help us.
First, we find the derivative of 
Also, the constant multiple rule will apply to the coefficients of each term. The constant multiple rule simply says that any constant factor of a term will "carry" to the derivative of that term. For example:
Lastly, the derivative of a constant is zero. This will result in the last term, 
Applying these rules, we find the derivative
Where the derivative is positive (blue line in graph), the tangent line to the original function is angled up. Where the derivative is negative (red line in graph), the slope of the tangent line is angled down.

The points where the tangent line's slope transitions from negative to positive or vice versa, are called the critical points. At these points, the tangent line becomes a horizontal line with a slope of zero (green line in graph). In other words, the "critical points" occur when the derivative is zero. These points will be the endpoints of our intervals of increasing and decreasing. To find the critical points, we will set the derivative equal to zero and solve for x. In this problem factoring is the best method:



Now that we have found the critical points, we need to know whether the original function is increasing or decreasing in the intervals between them. We will do so by testing a point in each interval and determining whether the derivative is positive or negative at that point. This is called the first derivative line test.
For the interval 

(Note: I will use the factored form of the derivative, but we could also use the polynomial version. Both will give the same result)
Since the derivative is negative at this point, we can conclude that the derivative is negative for the whole interval. Thus, the original function is decreasing on 
For the interval 

Since the derivative is positive at this point, we can again conclude that the derivative is positive for the whole interval. Thus, the original function is increasing on 
For the interval 

Since the derivative is negative at this point, we can again conclude that the derivative is negative for the whole interval. Thus, the original function is decreasing on 
Lastly, for the interval 

Since the derivative is positive at this point, we know that the derivative is positive for the whole interval. Thus the original function is increasing on 
From these 4 results, we now know the answer. The function is increasing on the intervals 
A right triangle has sides of lenght 

a) Find the rate at which the angle 

Explanation
A right triangle has sides of lenght 

Find the rate at which the angle 


a) First we need to write an expression for the angle 



Now we need to differentiate with respect to 
Recall the the general derivative for the inverse tangent function is:
Applying this to our function for 
Determine the rate of change of the angle opposite the base of a right triangle -whose length is increasing at a rate of 1 inch per minute, and whose height is a constant 2 inches - when the area of the triangle is 2 square inches.




Explanation
To determine the rate of the change of the angle opposite to the base of the given right triangle, we must relate it to the rate of change of the base of the triangle when the triangle is a certain area.
First we must determine the length of the base of the right triangle at the given area:
Now, we must find something that relates the angle opposite of the base to the length of the base and height - the tangent of the angle:
To find the rate of change of the angle, we take the derivative of both sides with respect to time, keeping in mind that the base of the triangle is dependent on time, while the height is constant:
We know the rate of change of the base, and we can find the angle from the sides of the triangle:
Plugging this and the other known information in and solving for the rate of change of the angle adjacent to the base, we get

Find the derivative of the following function at the point 
Explanation
Use the power rule on each term of the polynomial to get the derivative,
Now we plug in
Given that 
Explanation
To find the derivative of the function, we use implicit differentiation, which is an application of the chain rule. We use this because 



First, we use the chain rule combined with the product rule in taking the derivative of y
Then we expand in order to isolate the terms with
Then we factor out a




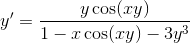







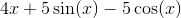





![speed(0)=3 [m/s]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012232/gif.latex)
![speed(2)=1[m/s]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012233/gif.latex)
![a(0)=2[m/s^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012234/gif.latex)
![a(2)=2[m/s^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012235/gif.latex)
![speed(0)=1 [m/s]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012236/gif.latex)
![speed(2)=3[m/s]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012237/gif.latex)
![a(0)=2[m/s^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012238/gif.latex)
![a(2)=2[m/s^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012239/gif.latex)
![speed(0)=3 [m/s]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012240/gif.latex)
![speed(2)=1[m/s]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012241/gif.latex)
![a(0)=-2[m/s^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012242/gif.latex)
![a(2)=-2[m/s^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012243/gif.latex)
![speed(0)=1 [m/s]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012244/gif.latex)
![speed(2)=3[m/s]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012245/gif.latex)
![a(0)=-2[m/s^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012246/gif.latex)
![a(2)=-2[m/s^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012247/gif.latex)
![speed(0)=3 [m/s]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012248/gif.latex)
![speed(2)=1[m/s]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012249/gif.latex)
![a(0)=2[m/s^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012250/gif.latex)
![a(2)=2[m/s^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012251/gif.latex)








![speed(0)=\left |v(0)\right |=3 [m/s]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012295/gif.latex)




![speed(2)=\left |v(2)\right |=1[m/s]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012300/gif.latex)




![=2 [m/s^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012305/gif.latex)












![\frac{\mathrm{d}}{\mathrm{d} x} [x^n] = n \cdot x^{n - 1}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/946872/gif.latex)
![\frac{\mathrm{d} }{\mathrm{d} x}[-8x^3]= -8 \cdot \frac{\mathrm{d} }{\mathrm{d} x}[x^3] = -8 \cdot 3x^2 = -24x^2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/946873/gif.latex)



![0 = 4 [ x^2(x - 6) - 3(x - 6)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/946878/gif.latex)
![0 = 4[(x-6)(x^2 - 3)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/946879/gif.latex)