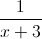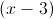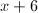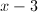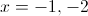How to find the solution of a rational equation with a binomial denominator
Help Questions
Algebra › How to find the solution of a rational equation with a binomial denominator
Solve for 




Explanation
The two fractions on the left side of the equation need a common denominator. We can easily do find one by multiplying both the top and bottom of each fraction by the denominator of the other.




Now add the two fractions:
To solve, multiply both sides of the equation by 

Multiply both sides by 3:
Move all terms to the same side:
This looks like a complicated equation to factor, but luckily, the only factors of 37 are 37 and 1, so we are left with

Our solutions are therefore
and

Solve for 
Explanation
Multiply each side of the equation by
Distribute 5 to each term in parentheses.
Subtract 25 from each side of equation.
Divide each side of equation by 5.
Square root of each side of equation.
Simplify the expression:
Explanation
First, factor out x from the numerator:
Notice that the resultant expression in the parentheses is quadratic. This expression can be further factored:
We can then cancel the (x-3) which appears in both the numerator and denominator:
Finally, distribute the x outside of the parentheses to reach our answer:
Solve for 
Explanation
Multiply each side by
Distribute 3 to the terms in parentheses.
Subtract 6 from each side of the equation.
Divide each side by 3.
Solve for 
None of the other answers.
Explanation
Multiply each side by
Distribute 2 to each term of the polynomial.
Divide the polynomial by 6.
Divide each side by 6.
Subtract the 
Simplify:
Explanation
Factor out 
Hence we get the following
which is equal to
Simplify:
Explanation
If we factors the denominator we get
Hence the rational expression becomes equal to
which is equal to
For all values 
Explanation
First, factor the numerator. We need factors that multiply to 

We can plug the factored terms into the original expression.
Note that 
This is our final answer.
Which of the following fractions is NOT equivalent to 
Explanation
We know that 


By this property, there is no way to get 

Therefore the correct answer is 
Find the values of 
Explanation
If 

This happens when x = 1 or when x = -2.
Therefore the correct answer is