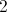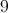How to find the solution for a system of equations
Help Questions
Algebra › How to find the solution for a system of equations
Use elimination to solve the solution:
Explanation
For elimination you need to get one variable by itself by cancelling the other out. In this equation this is best done by getting rid of 

then add the equations together
which, simplified, is
divied by 
Then plug 
Solve for 
Solve this system of equations:
Explanation
We can rewrite the first equation as:
If we substitute this new value for 
Simplify.
Combine like terms
Solve for
Now substitute this value into either of the original equations:
In the standard coordinate plane, slope-intercept form is defined for a straight line as 



Give the coordinates at which the following lines intersect:
The two lines do not intersect.
Explanation
The first step is to set the two equations equal to each other, since at the point of intersection, they will be. To do this more easily, convert each equation into slope-intercept form.
First equation:





Second equation:


Now, since each equation equals 









So, the 







So, the coordinates where the two lines intersect are 
Without drawing a graph of either equation, find the point where the two lines intersect.
Line 1 :
Line 2 :
Explanation
To find the point where these two lines intersect, set the equations equal to each other, such that 



Subtract 
Divide both sides by 2.
Now substitute 

With both coordinates, we know the point of intersection is 




In the standard coordinate plane, slope-intercept form is defined for a straight line as 



Give the coordinates at which the following lines intersect:
Explanation
The first step is to set the two equations equal to each other, since at the point of intersection, they will be. To do this more easily, convert each equation into slope-intercept form.
First equation:



Second equation:





Now, since each equation equals 








So, the 





So, the coordinates where the two lines intersect are 
Find the solution to this system of equations:
None of these
Explanation
To find the solution we will multiply by some number to cancel out one variable and then solve for the variable that is left over. This is called the "elimination" method. You may choose to eliminate either variable, but it is prudent to choose the variable that is easier to cancel.
Multiply equation 1 by -2:
Add new equation 1 to equation 2:
The result is
Solve for y:
Now solve for x by plugging in the value for y (we can choose either original equation):
Solve for 
The system has no solution
Explanation
In the second equation, you can substitute 

Now, substitute 2 for 
The solution is
Solve the following system of equation
Cannot be solved
Explanation
Start with the equation with the fewest variables, 
Solve for 
Plug this 

Subtract 10 from both sides:
Divide by 9:
Plug these 


Combine like terms:
Subtract 2:
Divide by -4:
Therefore the final solution is 
What is the sum of 

Explanation
Add the equations together.
Put the terms together to see that 
Substitute this value into one of the original equaitons and solve for 
Now we know that 


In the standard coordinate plane, slope-intercept form is defined for a straight line as 



Give the coordinates at which the following lines intersect:
The two lines do not intersect.
Explanation
The first step is to set the two equations equal to each other, since at the point of intersection, they will be. To do this more easily, convert each equation into slope-intercept form.
First equation:

Second equation:





At this point, note that both equations have idential slopes: 





Thus, there is no solution to this equation, and the lines are parallel.