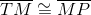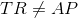Advanced Geometry

Help Questions

Geometry › Advanced Geometry

Questions 1 - 10

The sides of a square garden are 10 feet long. What is the area of the garden?

$140 ft^{2}$

$20ft^{2}$

$40ft^{2}$

$110ft^{2}$

Explanation

The formula for the area of a square is

$Area = s^{2}$

where is the length of the sides. So the solution can be found by

$Area=(10)^{2}=100 ft^{2}$

True or false: The graph of $f(x) = \frac{ x-7}{2x^{2}-15x+7}$ has as a vertical asymptote the graph of the equation .

False

True

Explanation

The vertical asymptote(s) of the graph of a rational function such as can be found by evaluating the zeroes of the denominator after the rational expression is reduced.

First, factor the numerator. It is a quadratic trinomial with lead term $2x^{2}$ , so look to factor

$2x^{2}-15x+7$

by using the grouping technique. We try finding two integers whose sum is and whose product is ; with some trial and error we find that these are and , so:

$2x^{2}-15x+7$

Break the linear term:

$=2x^{2}-x-14 x+7$

Regroup:

$=(2x^{2}-x )-(14 x-7)$

Factor the GCF twice:

Therefore, can be rewritten as

$f(x) = \frac{ x-7}{(x -7) (2 x-1)}$

Cancel the common factor from both halves; the function can be rewritten as

$f(x) = \frac{1}{ 2 x-1}$

Set the denominator equal to 0 and solve for :

$\frac{2x}{2}= \frac{1}{2}$

$x= \frac{1}{2}$

The graph of therefore has one vertical asymptotes, the line of the equations $x= \frac{1}{2}$ . The line of the equation is not a vertical asymptote.

Define $g (x) = \frac{1}{\sqrt[3]{x -27}}$

What is the natural domain of ?

$(-\infty , 27)\cup (27, \infty )$

$(27, \infty )$

$(3, \infty )$

$(-\infty , - 27)\cup (27, \infty )$

$(-\infty , - 3)\cup (3, \infty )$

Explanation

The radical in and of itself does not restrict the domain, since every real number has a real cube root. However, since the expression $\sqrt[3]{x -27}$ is in a denominator, it cannot be equal to zero, so the domain excludes the value(s) for which

$\sqrt[3]{x -27} = 0$

$\left (\sqrt[3]{x -27} \right )^{3}= 0^{3}$

27 is the only number excluded from the domain.

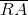
Given Trapezoid with bases $\overline{TR}$ and $\overline{AP}$ . The trapezoid has midsegment $\overline{MN}$ , where and are the midpoints of $\overline{TP}$ and $\overline{RA}$ , respectively.

True, false, or undetermined: Trapezoid $TRNM \sim$ Trapezoid .

False

True

Undetermined

Explanation

The fact that the trapezoid is isosceles is actually irrelevant. Since and are the midpoints of legs $\overline{TP}$ and $\overline{RA}$ , it holds by definition that

$\overline{TM} \cong \overline{MP}$

and

$\overline{RN} \cong \overline{NA}$

It follows that $\frac{TM}{MP} = \frac{RN}{NA} = 1$

However, the bases of each trapezoid are noncongruent, by definition, so, in particular,

$TR \ne AP$

Assume that 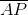$\overline{AP}$ is the longer base - this argument works symmetrically if the opposite is true. Let - equivalently, .

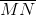
Since the bases are of unequal length, $x \ne 0$ . The length of the midsegment $\overline{MN}$ is the arithmetic mean of the lengths of these two bases, so

$MN = \frac{TR + AP}{2} = \frac{TR + TR + x }{2} = \frac{ 2 \cdot TR + x }{2} = TR + \frac{x}{2}$

Since $TR \ne MN$ , it follows that

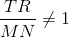
$\frac{TR}{MN} \ne 1$ ,

and

$\frac{TR}{MN} \ne \frac{TM}{MP} = \frac{RN}{NA}$ .

This disproves similarity, since one condition is that corresponding sides must be in proportion.

A rhombus has a side length of $\frac{5}{6}$ foot, what is the length of the perimeter (in inches).

inches

feet

inches

Explanation

To find the perimeter, first convert $\frac{5}{6}$ foot into the equivalent amount of inches. Since, $\frac{5}{6}=\frac{10}{12}$ and $\frac{12}{12}=1foot$ , $\frac{5}{6}$ is equal to inches.

Then apply the formula , where is equal to the length of one side of the rhombus.

Since,

The solution is:

Find the area of a square if its diagonal is $5\sqrt3$

$\frac{75}{2}$

$\frac{75\sqrt3}{2}$

$75\sqrt2$

$75\sqrt6$

Explanation

The diagonal of a square is also the hypotenuse of a triangle.

Recall how to find the area of a square:

$\text{Area}=\text{side}^2$

Now, use the Pythagorean theorem to find the area of the square.

$\text{side}^2+\text{side}^2=\text{Diagonal}^2$

$2(\text{side})^2=\text{Diagonal}^2$

$\text{side}^2=\frac{\text{Diagonal}^2}{2}$

$\text{Area}=\text{side}^2=\frac{\text{Diagonal}^2}{2}$

Plug in the length of the diagonal to find the area of the square.

$\text{Area}=\frac{(5\sqrt3)^2}{2}=\frac{75}{2}$

If the perimeter of a rectangle is , and the width of the rectangle is , what is the area of a rectangle?

Explanation

Recall how to find the perimeter of a rectangle:

$\text{Perimeter}=2(\text{length}+\text{width})$

Since we are given the width and the perimeter, we can solve for the length.

$\text{length}+\text{width}=\frac{\text{Perimeter}}{2}$

$\text{length}=\frac{\text{Perimeter}}{2}-\text{width}$

Substitute in the given values for the width and perimeter to find the length.

$\text{length}=\frac{36}{2}-17$

Simplify.

$\text{length}=18-17$

Solve.

$\text{length}=1$

Now, recall how to find the area of a rectangle.

$\text{Area}=\text{length}\times\text{width}$

Substitute in the values of the length and width to find the area.

$\text{Area}=17 \times 1$

Solve.

$\text{Area}=17$

In which quadrant does the complex number lie?

Explanation

If we graphed the given complex number on a set of real-imaginary axes, we would plot the real value of the complex number as the x coordinate, and the imaginary value of the complex number as the y coordinate. Because the given complex number is as follows:

We are essentially doing the same as plotting the point on a set of Cartesian axes. We move units right in the x direction, and units down in the y direction, which puts us in the fourth quadrant, or in terms of Roman numerals:

Find the area of the rhombus.

Explanation

Recall that one of the ways to find the area of a rhombus is with the following formula:

$\text{Area}=\text{base}\times\text{height}$

Now, since all four sides in the rhombus are the same, we know from the given side value what the length of the base will be. In order to find the length of the height, we will need to use sine.

$\sin x=\frac{\text{height}}{\text{side}}$ , where is the given angle.