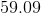Acute / Obtuse Triangles
Help Questions
ACT Math › Acute / Obtuse Triangles

What is the value of 
Cannot be calculated
Explanation
Begin by filling in the missing angle for your triangle. Since a triangle has a total of 
Draw out the figure:

Now, to solve this, you will need some trigonometry. Use the Law of Sines to calculate the value:
Solving for 
Rounding, this is 

What is the value of 
Cannot be calculated
Explanation
Begin by filling in the missing angle for your triangle. Since a triangle has a total of 
Draw out the figure:

Now, to solve this, you will need some trigonometry. Use the Law of Sines to calculate the value:
Solving for 
Rounding, this is 
In a given triangle, the angles are in a ratio of 1:3:5. What size is the middle angle?
Explanation
Since the sum of the angles of a triangle is 

If the smallest angle is 20 degrees, then given that the middle angle is in ratio of 1:3, the middle angle would be 3 times as large, or 60 degrees.

What is the value of 
Cannot be computed
Explanation
What is the value of 
Begin by filling in the missing angle for your triangle. Since a triangle has a total of 
Draw out the figure:

Now, to solve this, you will need some trigonometry. Use the Law of Sines to calculate the value:
Solving for 
Rounding, this is 

What is the value of 
Cannot be computed
Explanation
What is the value of 
Begin by filling in the missing angle for your triangle. Since a triangle has a total of 
Draw out the figure:

Now, to solve this, you will need some trigonometry. Use the Law of Sines to calculate the value:
Solving for 
Rounding, this is 
In a given triangle, the angles are in a ratio of 1:3:5. What size is the middle angle?
Explanation
Since the sum of the angles of a triangle is 

If the smallest angle is 20 degrees, then given that the middle angle is in ratio of 1:3, the middle angle would be 3 times as large, or 60 degrees.

What is the value of 
Cannot be computed
Explanation
Begin by filling in the missing angle for your triangle. Since a triangle has a total of 
Draw out the figure:

Now, to solve this, you will need some trigonometry. Use the Law of Sines to calculate the value:
Solving for 
Rounding, this is 

What is the value of 
Cannot be computed
Explanation
Begin by filling in the missing angle for your triangle. Since a triangle has a total of 
Draw out the figure:

Now, to solve this, you will need some trigonometry. Use the Law of Sines to calculate the value:
Solving for 
Rounding, this is 
There are two similar triangles. One has side lengths of 14, 17, and 19. The smaller triangle's smallest side length is 2. What is the length of its longest side?
Explanation
Use proportions to solve for the missing side:
Cross multiply and solve:

What is the length of side 
Cannot be computed
Explanation
Begin by filling in the missing angle for your triangle. Since a triangle has a total of 
Draw out the figure:

This problem becomes incredibly easy! This is an isosceles triangle. Therefore, you know that