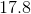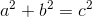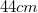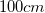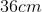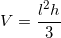Pyramids
Help Questions
ACT Math › Pyramids
Find the surface of a isoceles pyramid whose height is 


Explanation
To find surface area of a pyramid, simply find the surface area of each of the faces and add them together.
Since there are 4 trangular faces, we have to multiply that surface area by 4. Thus,
Find the surface of a isoceles pyramid whose height is 


Explanation
To find surface area of a pyramid, simply find the surface area of each of the faces and add them together.
Since there are 4 trangular faces, we have to multiply that surface area by 4. Thus,
A square pyramid has a slant height of 8. The edge of a face is 12. What is the measure of an edge of its base?
Explanation
In this kind of a problem, it's helpful to draw out all information that's given.
Because the triangular faces of a pyramid are isosceles triangles, the slant height can be seen to divide it into two right triangles. The goal is to find the measure of the edge of the square base. This quickly becomes a problem revolving around the use of the Pythagorean theorem.
If we take the measures 12 and 8 to be the hypotenuse and one of the legs, respectively, we can use the Pythagoream theorem to solve for the "base leg." Then, realizing that this measure if only half of the the total length of the square base edge, that value must be multiplied by 2.
Therefore,
A square pyramid has a slant height of 8. The edge of a face is 12. What is the measure of an edge of its base?
Explanation
In this kind of a problem, it's helpful to draw out all information that's given.
Because the triangular faces of a pyramid are isosceles triangles, the slant height can be seen to divide it into two right triangles. The goal is to find the measure of the edge of the square base. This quickly becomes a problem revolving around the use of the Pythagorean theorem.
If we take the measures 12 and 8 to be the hypotenuse and one of the legs, respectively, we can use the Pythagoream theorem to solve for the "base leg." Then, realizing that this measure if only half of the the total length of the square base edge, that value must be multiplied by 2.
Therefore,
A square pyramid has a volume of 
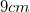
Explanation
The formula for the volume of a pyramid is:
We know that 








This gives us a new equation of:
We then plug in the variables we know:
Multiply both sides by 3:
Divide both sides by 9:
Therefore, we now know that the length of the pyramid's base is 

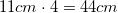

A square pyramid has a volume of 
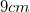
Explanation
The formula for the volume of a pyramid is:
We know that 








This gives us a new equation of:
We then plug in the variables we know:
Multiply both sides by 3:
Divide both sides by 9:
Therefore, we now know that the length of the pyramid's base is 

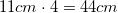

What is the surface area of a square pyramid with a height of 12 in and a base side length of 10 in?
Explanation
The surface area of a square pyramid can be broken into the area of the square base and the areas of the four triangluar sides. The area of a square is given by:
The area of a triangle is:
The given height of 12 in is from the vertex to the center of the base. We need to calculate the slant height of the triangular face by using the Pythagorean Theorem:
where 

So, the area of the triangle is:
There are four triangular sides totaling 
The total surface area is thus 
What is the surface area of a square pyramid with a height of 12 in and a base side length of 10 in?
Explanation
The surface area of a square pyramid can be broken into the area of the square base and the areas of the four triangluar sides. The area of a square is given by:
The area of a triangle is:
The given height of 12 in is from the vertex to the center of the base. We need to calculate the slant height of the triangular face by using the Pythagorean Theorem:
where 

So, the area of the triangle is:
There are four triangular sides totaling 
The total surface area is thus 
An architect wants to make a square pyramid and fill it with 12,000 cubic feet of sand. If the base of the pyramid is 30 feet on each side, how tall does he need to make it?
Explanation
Volume of Pyramid = 1/3 * Area of Base * Height
12,000 ft3 = 1/3 * 30ft * 30ft * H
12,000 = 300 * H
H = 12,000 / 300 = 40
H = 40 ft
An architect wants to make a square pyramid and fill it with 12,000 cubic feet of sand. If the base of the pyramid is 30 feet on each side, how tall does he need to make it?
Explanation
Volume of Pyramid = 1/3 * Area of Base * Height
12,000 ft3 = 1/3 * 30ft * 30ft * H
12,000 = 300 * H
H = 12,000 / 300 = 40
H = 40 ft