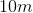Other Quadrilaterals
Help Questions
ACT Math › Other Quadrilaterals
The sides of rectangle A measure to 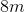
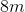

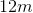
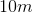
Explanation
In similar rectangles, the ratio of the sides must be equal.
To solve this question, the following equation must be set up:


We then must cross multiply, which leaves us with:
Lastly, we divide both sides by 8 to solve for the missing side:
Therefore, the longer sides of the rectangle are each 
The sides of rectangle A measure to 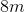
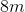

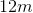
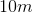
Explanation
In similar rectangles, the ratio of the sides must be equal.
To solve this question, the following equation must be set up:


We then must cross multiply, which leaves us with:
Lastly, we divide both sides by 8 to solve for the missing side:
Therefore, the longer sides of the rectangle are each 
A square has a length of 
Explanation
A square with a length of 

A square has a length of 
Explanation
A square with a length of 

Suppose a rectangle has side lengths of 7 and 3. Another rectangle has another set of side lengths that are 8 and 4. Are these similar rectangles, and why?
Explanation
Set up the proportion to determine if the ratios of both rectangles are equal.
If they are, then they are similar.
These are not similar rectangles since their ratios are not the same.
Suppose a rectangle has side lengths of 7 and 3. Another rectangle has another set of side lengths that are 8 and 4. Are these similar rectangles, and why?
Explanation
Set up the proportion to determine if the ratios of both rectangles are equal.
If they are, then they are similar.
These are not similar rectangles since their ratios are not the same.

The rhombus above is bisected by two diagonals.
If 


Note: The shape above may not be drawn to scale.
Explanation
A rhombus is a quadrilateral with two sets of parallel sides as well as equal opposite angles. Since the lines drawn inside the rhombus are diagonals, 

Therefore, 
Thus,
Since 


The rhombus above is bisected by two diagonals.
If 


Note: The shape above may not be drawn to scale.
Explanation
A rhombus is a quadrilateral with two sets of parallel sides as well as equal opposite angles. Since the lines drawn inside the rhombus are diagonals, 

Therefore, 
Thus,
Since 


Find the perimeter of the rhombus above.
Explanation
By definition, a rhombus is a quadrilateral with four equal sides whose angles do not all equal 90 degrees. To find the perimeter, we must find the values of x and y. In order to do so, we must set up a system of equations where we set two sides equal to each other. Any two sides can be used to create these systems.
Here is one example:
Eq. 1
Eq. 2
Now we plug 

Plugging these values into any of the three equations will give us the length of one side equaling 11.
Since there are four sides, 

Find the perimeter of the rhombus above.
Explanation
By definition, a rhombus is a quadrilateral with four equal sides whose angles do not all equal 90 degrees. To find the perimeter, we must find the values of x and y. In order to do so, we must set up a system of equations where we set two sides equal to each other. Any two sides can be used to create these systems.
Here is one example:
Eq. 1
Eq. 2
Now we plug 

Plugging these values into any of the three equations will give us the length of one side equaling 11.
Since there are four sides,