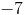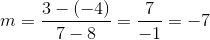Other Lines
Help Questions
ACT Math › Other Lines
What is the slope of a line which passes through coordinates 

Explanation
Slope is found by dividing the difference in the 

Consider the lines described by the following two equations:
4y = 3x2
3y = 4x2
Find the vertical distance between the two lines at the points where x = 6.
36
21
12
44
48
Explanation
Since the vertical coordinates of each point are given by y, solve each equation for y and plug in 6 for x, as follows:

Taking the difference of the resulting y -values give the vertical distance between the points (6,27) and (6,48), which is 21.
What is the slope of a line which passes through coordinates 

Explanation
Slope is found by dividing the difference in the 

Consider the lines described by the following two equations:
4y = 3x2
3y = 4x2
Find the vertical distance between the two lines at the points where x = 6.
36
21
12
44
48
Explanation
Since the vertical coordinates of each point are given by y, solve each equation for y and plug in 6 for x, as follows:

Taking the difference of the resulting y -values give the vertical distance between the points (6,27) and (6,48), which is 21.
What is the slope of a line that passes though the coordinates 

Explanation
The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.
Use the give points in this formula to calculate the slope.
What is the slope of a line that passes though the coordinates 

Explanation
The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.
Use the give points in this formula to calculate the slope.
What is the slope of a line running through points 

Explanation
The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.
Use the give points in this formula to calculate the slope.
What is the slope of a line running through points 

Explanation
The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.
Use the give points in this formula to calculate the slope.
Let y = 3_x_ – 6.
At what point does the line above intersect the following:
They do not intersect
They intersect at all points
(0,–1)
(–5,6)
(–3,–3)
Explanation
If we rearrange the second equation it is the same as the first equation. They are the same line.
Let y = 3_x_ – 6.
At what point does the line above intersect the following:
They do not intersect
They intersect at all points
(0,–1)
(–5,6)
(–3,–3)
Explanation
If we rearrange the second equation it is the same as the first equation. They are the same line.