How to multiply polynomials
Help Questions
ACT Math › How to multiply polynomials
Two positive consecutive whole numbers that are even are both multiples of 

Explanation
The question provides two positive whole numbers that are each multiples of 6 and also 6 numbers apart. This may be translated into variables, where the first number may be represented by "x" and the second number may be represented as "x+6" given that it is 6 numbers greater than x.
The problem provides the information that the product of these two numbers is 72. Using the new definitions for the numbers, this may be represented as:
(x)(x+6) = 72
This provides an equation that multiplies two polynomials (one with one term, which is a monomial and one with two terms, which is a binomial) and an ability to solve for what x (the first of the two numbers) may be.
Using FOIL, the result is 


The final step of the problem is to solve for the sum of these two numbers:
6+12=18
Expand:
Explanation
Expand:
Step 1: Use the distributive property
Step 2: Combine like terms
Multiply these polynomials out and expand.
Explanation
The proper way to multiply polynomials is to essentially apply the distributive property continually.
So 
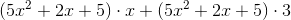
Then, simply group together like terms to get the final answer: