How to find the union of a Venn Diagram
Help Questions
ACT Math › How to find the union of a Venn Diagram

In the venn diagram above, let the set 


Explanation



In a class of senior high-school students, 



Explanation
A Venn diagram can help us determine the total number of students in the class.
First, we must calculate the number of students who have ONLY cats or ONLY dogs. First, for cats, 15 students have cats, and 5 students have both cats and dogs.
Ten students have only cats.
For dogs, 12 students have dogs, and 5 students have both cats and dogs.
Seven students have only dogs.
Using this information, we can fill in the Venn diagram.

This diagram shows the 10 students with only cats, the 7 students with only dogs, the 5 students with both, and the 8 students with neither. Adding up the numbers will give us the total number of students.
In a venn diagram, let 
What is
Explanation






A group of high school juniors are taking Biology, Calculus, and Spanish as shown above. Which student is not in the set 
Patrick
Molly
Bob
Steph
Andy
Explanation
The notation 


Giving the Venn diagram above, what is the sum of the numbers in the set 
Explanation
The notation 


When we add the numbers together, we get:
Given the Venn diagram below, which of the following does not belong to 
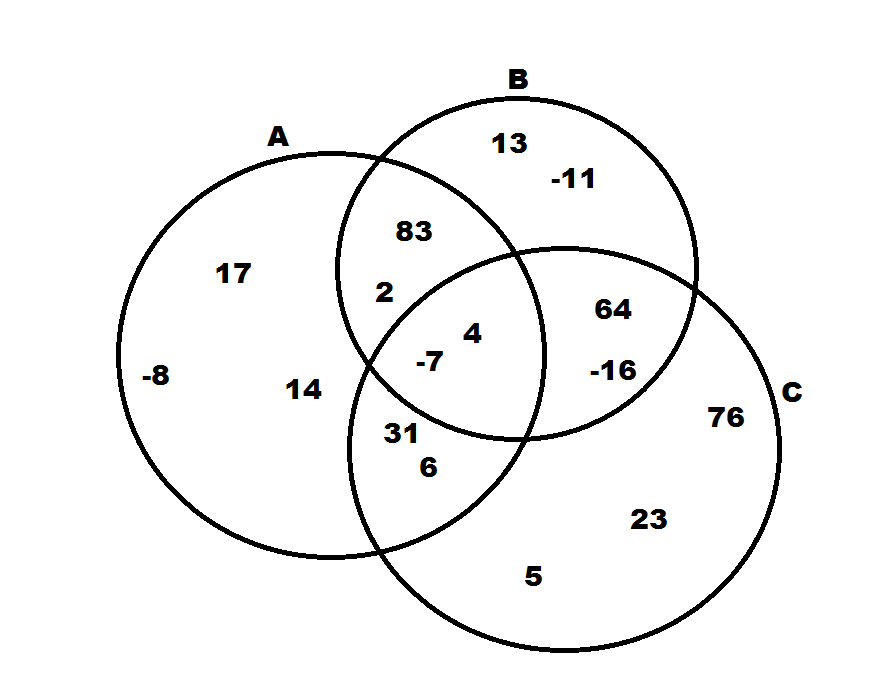
Explanation
The symbol 

Sixty high school seniors were polled to see if they were taking history and calculus. A total of 29 students said they were taking calculus, and a total of 50 students said they were taking history. What is the minimum number of students who take both history and calculus?
Explanation
We can draw a Venn diagram to see these two sets of students.

We need to find the overlap between these two sets. To find that, add up the total number of students who are taking history and the total number of students who are taking calculus.
Notice that we have more students this way than the total number who were polled. That is because the students who are taking history AND calculus have been double counted. Subtract the total number of students polled to find out how many students were counted twice.
Forty students play soccer and/or basketball after school. Twenty-four students play soccer and twenty-nine play basketball. How many students play both soccer and basketball?
Explanation
We can draw a Venn diagram of these students.

Drawn this way, there are more students on the Venn diagram than we have.
This is because some of the students play both sports and should be in the overlap on the Venn diagram. To find the number of students in the overlap, subtract the total number of students given from the number on the diagram.
This represents the number of students who were counted twice, or the number in the overlap.
We can redraw the correct Venn diagram with this number.

















































