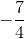How to find the slope of a tangent line
Help Questions
ACT Math › How to find the slope of a tangent line
Find the slope of the tangent line to 

Explanation
To find the slope of the tangent line, we must take the derivative.
By using the Power Rule we will be able to find the derivative:
Therefore derivative of 

Now we plug in 

There is a circle on a coordinate plain. Its perimeter passes through the point 

Explanation
In this kind of problem, it's important to keep track of information given about your line of interest. In this case, the coordinates given set up the stage for us to be able to get to our line of focus - the line perpendicular to the tangent line. In order to determine the perpendicular line's slope, the tangent line's slope must be calculated. Keeping in mind that:
where y2,x2 and y1,x1 are assigned arbitrarily as long as the order of assignment is maintained.

To calculate the perpendicular line, we have to remember that the product of the tangent slope and the perpendicular slope will equal -1.

A line runs tangent to a circle at the point 
Cannot be determined
Explanation
The only two bits of information that are given for the tangent line is that it runs through the points 

where 




Slope can be calculated through substituting in for the given values: