How to find the intersection of a Venn Diagram
Help Questions
ACT Math › How to find the intersection of a Venn Diagram
Set A contains the positive even integers less than 14. Set B contains the positive multiples of three less than 20. What is the intersection of the two sets?
A∩B = { }
A∩B = {6, 12}
A∩B = {4, 6, 8}
A∩B = {6}
A∩B = {6, 12, 18}
Explanation
A = {2, 4, 6, 8, 10, 12}
B = {3, 6, 9, 12, 15, 18}
The intersection of a set means that the elements are in both sets: A∩B = {6, 12}
There are 75 juniors at a high school. 15 of the students are enrolled in Physics and 40 students are enrolled in Chemistry. 30 students are not enrolled in either Physics or Chemistry. How many students are enrolled in both Physics and Chemistry?
30
25
15
10
5
Explanation
First, subtract the students that are in neither class; 75 – 30 = 45 students.
Thus, 45 students are enrolled in Chemistry, Physics, or both. Of these 45 students, we know 40 are in Chemistry, so that leaves 5 students who are enrolled in Physics only; with 15 total students in Physics, that means 10 must be in Chemistry as well. So 10 students are in both Physics and Chemistry.

In the Venn Diagram shown above, let 



Explanation








Since the universe is integers less than or equal to 10, we see that the only ones that fit that description that are not in 
Students at a local high school are given the option to take one gym class, one music class or one of each. Out of 100 students, 60 say that they are currently taking a gym class and 70 say that they are taking a music class. How many students are taking both?
Explanation
This problem can be solved two ways, with a formula or with reason.
Using the formula, the intersection of the Venn diagram for which classes students take is:
By using reason, it is clear that 60 + 70 is greater than 100 by 30. It is assumed that this extra 30 students come from students who were counted twice because they took both classes.
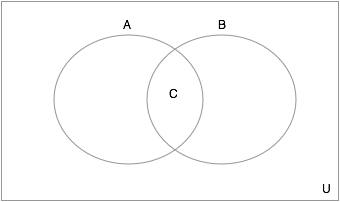
In the Venn Diagram shown above, let the set 





Explanation
To find the intersection of a set of numbers, we need to find all numbers that are in both sets (definition of intersection). We can see that all the primes less than 

Fifty 6th graders were asked what their favorite school subjects were. Three students like math, science and English. Five students liked math and science. Seven students liked math and English. Eight people liked science and English. Twenty students liked science. Twenty-eight students liked English. Fourteen students liked math. How many students didn’t like any of these classes?
10
7
5
3
None of the answers are correct
Explanation
Draw a Venn diagram with three subsets: Math, Science, and English. Start in the center with students that like all three subjects. Next, look at students that liked two subjects. Be sure to subtract out the ones already counted in the middle. Then, look at the students that only like one subject. Be sure to subtract out the students already accounted for. Once all of the subsets are filled, look at those students who don’t like any of these subjects. To find the students who don’t like any of these subjects add all of the students who like at least one subject from the total number of students surveyed, which is 50.
M = math
S = science
E = English
M∩S∩E = 3
M∩S = 5 (but 3 are already accounted for) so 2 for M and S ONLY
M∩E = 7 (but 3 are already accounted for) so 4 for M and E ONLY
S∩E = 8 (but 3 are already accounted for) so 5 for S and E ONLY
M = 14 (but 3 + 2 + 4 are already accounted for) so 5 for M ONLY
S = 20 (but 3 + 2 + 5 are already accounted for) so 10 for S ONLY
E = 28 (but 3 + 4 + 5 are already accounted for) so 16 for E ONLY
Therefore, the students already accounted for is 3 + 2 +4 + 5 + 5 + 10 + 16 = 45 students
So, those students who don’t like any of these subjects are 50 – 45 = 5 students
























