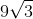How to find the area of a right triangle
Help Questions
ACT Math › How to find the area of a right triangle
A right triangle has integer sides with a ratio of 

Explanation
The easiest way to find the smallest possible integer sides is to simply factor the ratio we are given. In this case, 



The area of a triangle is expressed as 





Applying our formula, we get:
Thus, the smallest possible area for our triangle is 
A right triangle has a total perimeter of 12, and the length of its hypotenuse is 5. What is the area of this triangle?
3
6
10
12
15
Explanation
The area of a triangle is denoted by the equation 1/2 b x h.
b stands for the length of the base, and h stands for the height.
Here we are told that the perimeter (total length of all three sides) is 12, and the hypotenuse (the side that is neither the height nor the base) is 5 units long.
So, 12-5 = 7 for the total perimeter of the base and height.
7 does not divide cleanly by two, but it does break down into 3 and 4,
and 1/2 (3x4) yields 6.
Another way to solve this would be if you recall your rules for right triangles, one of the very basic ones is the 3,4,5 triangle, which is exactly what we have here
Find the area of a right triangle whose height is 4 and base is 5.
Explanation
To solve, simply use the formula for the area of a triangle given height h and base B.
Substitute


Thus,
The length of one leg of an equilateral triangle is 6. What is the area of the triangle?
Explanation
The base is equal to 6.
The height of an quilateral triangle is equal to 

The ratio for the side lengths of a right triangle is 3:4:5. If the perimeter is 48, what is the area of the triangle?
50
48
96
108
240
Explanation
We can model the side lengths of the triangle as 3x, 4x, and 5x. We know that perimeter is 3x+4x+5x=48, which implies that x=4. This tells us that the legs of the right triangle are 3x=12 and 4x=16, therefore the area is A=1/2 bh=(1/2)(12)(16)=96.
Find the area of the following right triangle to the nearest integer 
Note: The triangle is not necessarily to scale
None of the other answers
Explanation
The equation used to find the area of a right triangle is: 

Using the given information, we can write 


Right triangle 



Round angles to four significant figures. Round side lengths to the nearest integer.
Explanation
To find the area of a right triangle, find the lengths of the two perpendicular legs (since this gives us our length and height for the area formula).
In this case, we know that one angle is 








So with our two legs solved for, we now only need to apply the area formula for triangles to get our answer:
So, the area of our triangle is 

In the above triangle, if 

Explanation
To find the area of a triangle use the formula: