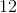How to find the angle of clock hands
Help Questions
ACT Math › How to find the angle of clock hands
How many degrees are in each hour-long section of an analog clock with 8 equally spaced numbers on the face?
Explanation
If creating a picture helps, draw a circle and place 8 at the top where 12 normally is. Then put 2, 4, and 6 at the positions of 3, 6, and 9 on a normal 12-hour analog clock. 1, 3, 5, and 7 go halfway in between each even number.
Now, because each section is equally spaced, and because there are 8 sections we simply divide the total number of degrees in a circle (
What is the measure, in degrees, of the acute angle formed by the hands of a 12-hour clock that reads exactly 3:10?
35°
55°
60°
65°
72°
Explanation
The entire clock measures 360°. As the clock is divided into 12 sections, the distance between each number is equivalent to 30° (360/12). The distance between the 2 and the 3 on the clock is 30°. One has to account, however, for the 10 minutes that have passed. 10 minutes is 1/6 of an hour so the hour hand has also moved 1/6 of the distance between the 3 and the 4, which adds 5° (1/6 of 30°). The total measure of the angle, therefore, is 35°.
What is the angle between the clock hands when the clock reads 6:30?
Explanation
Remember there are 

When the clock reads 6:30 the minute hand is on the 6, and the hour hand is halfway between the 6 and 7.
Thus the number of degrees between the hands is
It is 4 o’clock. What is the measure of the angle formed between the hour hand and the minute hand?
Explanation
At four o’clock the minute hand is on the 12 and the hour hand is on the 4. The angle formed is 4/12 of the total number of degrees in a circle, 360.
4/12 * 360 = 120 degrees
What is the angle of the major arc between the minute and hour hands of a clock reading 

Explanation
To find angular distance between the minute and hour hand, first find the position of each. Using 
First, remember that a circle contains 

For the hour hand, each hour in a 12-hour cycle takes up 

Thus, our distance from 


Likewise, our distance from 


Then, all we need to do is find the positive difference between these two measurements, 
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
Thus, the hands are 

What is the measure of the angle between the hands of a clock at 
Explanation
Each section of the clock is 










What is the angle of the major arc between the minute and hour hands of a clock reading 

Explanation
To find angular distance between the minute and hour hand, first find the position of each. Using 
First, remember that a circle contains 

For the hour hand, each hour in a 12-hour cycle takes up 

Thus, our distance from 


Likewise, our distance from 


Then, all we need to do is find the positive difference between these two measurements, 
This looks more complicated than it is! Fortunately, once our equation is set up, the problem is as easy as plug and play. First, let's find the measure of the minor arc between the minute hand and the reference. We can ignore hours (as each hour returns the minute hand to our reference angle) and just look at minutes.
Now, find the same distance, but for the hour hand. Here, we must consider both hours and minutes by using a fraction:
Lastly, we find the difference between these two references (remembering that our answer should be positive):
The problem asked for the major arc, so our answer is actually
Thus, the hands are 

A watch's hands move from 

Explanation
First, remember that a circle contains 

Thus, our total distance from our reference angle can be found as 

In this case, we simply find the difference of the two times, remembering to first convert hours to minutes:
Now, plug our answer in minutes into our equation:
So, our minute hand has moved 
Using the 8 hour analog clock from question 1 (an analog clock with 8 evenly spaced numbers on its face, with 8 where 12 normally is), what is the angle between the hands at 1:30? (Note: calculate the smaller angle, the one going between the hour and minute hand in a clockwise direction.)
Explanation
Because it's an 8 hour clock, each section of the clock has an angle of 45 degrees due to the fact that 
When the clock reads 1:30 the hour hand is halfway in between the 1 and the 2, and the minute hand is on the 4 (at the bottom of the clock). Therefore, between the hour hand and the "2" on the clock there are 

On a standard analog clock, what is the angle between the hands when the clock reads 
Explanation
To find the degrees of a clock hand, first find the angle between each hour-long sections. Since there are 







There are