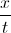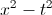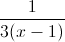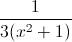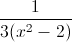How to divide rational expressions
Help Questions
ACT Math › How to divide rational expressions
Simplify the expression, leaving no radicals in the denominator:
Explanation
The easy way to solve this problem is to multiply both halves of the fraction by the conjugate of the denominator, since this will eliminate the radical in the denominator.

Next, simplify the fraction, eliminating any terms you can along the way.
Thus, 
Simplify the following expression:
Explanation
There are a couple ways to go about solving this problem. One could simply take the reciprocal of the second fraction, multiply everything out, and then look for ways to simplify. However, it is almost always easier to simplify before doing any multiplying.
To begin, we need to take the reciprocal of the second fraction, so that our expression becomes:
Then, before we multiply anything out, try to factor out the different parts of this expression. If we have any common factors in the numerator and denominator, we can cancel them out. In this case, the above expression factors as follows:
Conveniently, we can cancel out a bunch of factors here!
The common factors are highlighted in corresponding colors. We can actually cancel everything out here. We have a 



The reason we can cancel out terms when they are in the numerator and denominator is that we are essentially multiplying and then dividing by the same term. Since multiplication and division are opposite operations, they cancel each other out and we are left with 
Important side note: you can only cancel across two different fractions when you are multiplying and/or dividing. You CANNOT cancel factors across fractions if you are adding or subtracting them.
Simplify the expression, leaving no radicals in the denominator:
Explanation
The easy way to solve this problem is to multiply both halves of the fraction by the conjugate of the denominator, since this will eliminate the radical in the denominator.

Next, simplify the fraction, eliminating any terms you can along the way.
Thus, 
Simplify the expression:
Explanation
To begin, factor out the greatest common factor from each of the binomials to check for compatibility:

Next, eliminate the common factors and simplify.

Lastly, clean up the fraction.
Thus, our answer is 
Simplify:
Explanation
To begin, factor out the greatest common factor from each of the binomials to check for compatibility:

Next, eliminate the common factors and simplify.

Lastly, clean up the fraction.
Thus, our answer is 
Which of the following is equivalent to 
Explanation
We will need to simplify the expression 


In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. 

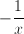


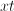
In order to convert the fraction 
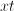

Similarly, we will multiply the top and bottom of 

We can now rewrite 

Let's go back to the original fraction 

To simplify this further, we can think of 


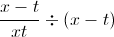
Lastly, we will use the property of exponents which states that, in general, 
The answer is 
What is 
Explanation




Simplify the expression:
Explanation
This problem looks intimidating, but can be solved with our standard tool; factoring the GCF out of each binomial.
Eliminate the obvious binomial:
But we're not through yet! Notice that we can further simplify this fraction:
Eliminate another pair, and the solution is now obvious:
Thus, our answer is 
Simplify the expression, leaving no radicals in the denominator:
Explanation
The easy way to solve this problem is to multiply both halves of the fraction by the conjugate of the denominator, since this will eliminate the radical in the denominator.

Next, simplify the denominator, eliminating any terms you can along the way.
Thus, 
Simplify:
Explanation
Multiply by the reciprocal of 
Factor
Divide by common factors.