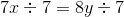Rhombuses
Help Questions
ISEE Upper Level Quantitative Reasoning › Rhombuses
Which is the greater quantity?
(a) The sum of the measures of the exterior angles of a thirty-sided polygon, one per vertex
(b) The sum of the measures of the exterior angles of a forty-sided polygon, one per vertex
(a) and (b) are equal
It is impossible to tell from the information given
(a) is greater
(b) is greater
Explanation
The Polygon Exterior-Angle Theorem states that the sum of the measures of the exterior angles of any polygon, one per vertex, is 



Which is the greater quantity?
(a) The perimeter of
(b) The perimeter of
It is impossible to tell from the information given.
(a) and (b) are equal.
(a) is greater.
(b) is greater.
Explanation
No information is given about the legs of either triangle; therefore, no information about their perimeters can be deduced.
In Rhombus 


(A)
(B)
(a) is the greater quantity
(b) is the greater quantity
It cannot be determined which of (a) and (b) is greater
(a) and (b) are equal
Explanation
The four sides of a rhombus, by defintion, have equal length, so
Since 
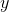

A rectangle is two feet longer than it is wide; its perimeter is 11 feet. What is its area in square inches?
It is impossible to determine the area from the information given
Explanation
The length of the rectangle is 2 feet, or 24 inches, greater than the width, so, if 

The perimeter of the rectangle is 11 feet, or 

The width is 21 inches, and the length is 45 inches. The area is their product:

The area of a rectangle is 4,480 square inches. Its width is 70% of its length.
What is its perimeter?
It is impossible to determine the area from the given information.
Explanation
If the width of the rectangle is 70% of the length, then

The area is the product of the length and width:
The perimeter is therefore

Which quantity is greater?
(a) The perimeter of a square with area 10,000 square centimeters
(b) The perimeter of a rectangle with area 8,000 square centimeters
It is impossible to tell from the information given
(a) and (b) are equal
(b) is greater
(a) is greater
Explanation
A square with area 10,000 square centimeters has sidelength 

Not enough information is given about the rectangle with area 8,000 square centimeters to determine its perimeter. For example, if its dimensions are 100 centimeters by 80 centimeters, its perimeter is 


The above diagram depicts trapezoid 
(a)
(b)
(a) and (b) are equal.
(a) is greater.
(b) is greater.
It is impossible to tell from the information given.
Explanation





The Same-Side Interior Angles Theorem states that if two parallel lines are crossed by a transversal, then the sum of the measures of a pair of same-side interior angles is always 
Therefore, 
Given Trapezoid 

Which is the greater quantity?
(a)
(b)
(a) is greater
(b) is greater
(a) and (b) are equal
It is impossible to tell from the information given
Explanation




The Same-Side Interior Angles Theorem states that if two parallel lines are crossed by a transversal, then the sum of the measures of a pair of same-side interior angles is always 


Substitute:
(a) is the greater quantity
A hexagon has six angles with measures
Which quantity is greater?
(a)
(b) 240
(a) and (b) are equal
(a) is greater
(b) is greater
It is impossible to tell from the information given
Explanation
The angles of a hexagon measure a total of 
The quantities are equal.
In Rhombus 


(A)
(B)
(a) is the greater quantity
(b) is the greater quantity
It cannot be determined which of (a) and (b) is greater
(a) and (b) are equal
Explanation
The four sides of a rhombus, by defintion, have equal length, so
Since